はじめに
筆者は業務上、過去の異なる要素の実績データから回帰直線を作成して予測値を算出し、検討資料に用いることがあります。
手計算でやると面倒で時間がかかってしまうのですが、エクセル関数を用いるととても簡単に回帰直線の傾きと切片を計算することができます。
この記事では、既知のyと既知のyのデータから傾きを計算するエクセル関数SLOPE関数と切片を計算するエクセル関数INTERCEPT関数について図と擬人化キャラクターのイラストを用いて解説します!
SLOPE関数とINTERCEPT関数の擬人化キャラクター

今日は私がいつもお世話になっているエクセル関数を紹介します!

どんな関数ですか?

正確にはお世話になっているエクセル関数たちですね。
SLOPE関数とINTERCEPT関数です。

いままで一度も見たことがないです・・・。

用途が限られているので見かけることが少ないかもしれませんね。
それでは、今回もエクセル関数ご本人たちに登場頂きましょう!


私はSLOPE関数!与えられたyの数値とxの数値から回帰直線の傾きを教えるよ!

私はINTERCEPT関数です。与えられたyの数値とxの数値から回帰直線の切片を教えます。

???

いきなり傾き、切片ではちょっと分からないですよね。

ベネ!下の図を見て下さい!
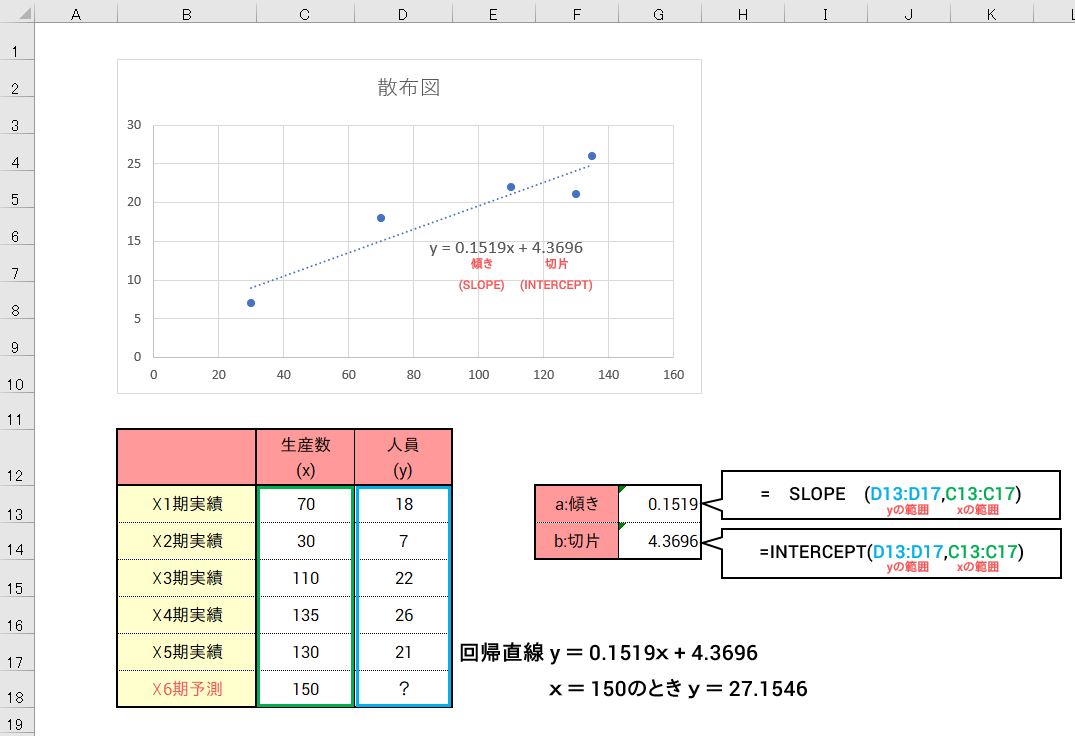

この図の例ではX1期からX5期までの生産数と人員の実績を元に、生産数150個が見込まれるX6期の人員予測を計算しようとしています・・・。

予測を計算!?そんなことができるんですか?

できるんですよ~!
図の上部にある散布図を見て下さい。
丸い点が下の表のX1期からX5期までの生産数と人員の散布を表しています。

縦(y)軸に人員、横(x)軸に生産数をとった散布になってるよ!

なるほど・・・。
当然といえば当然ですけど、生産数が多いとそれに応じて人員もたくさん必要と言える散らばり方ですね。

こういうのを正の相関性がある、なんて言いますね。

この点と点の相関をベネ(良い)な感じに表す直線があれば、生産数150個の時に人員数が何人くらいになるか分かりそうじゃない??

たしかに、横(x)軸の150から真上に上がっていって、その直線と交わる点から縦(y)軸を見れば人員の数がわかりそうです。

このベネな感じの直線はy = ax + bという式で表すことができます。

ええと・・・念の為補足すると関数さん達の言うベネな感じの直線は「回帰直線」って言います。

この式のa(傾き)を計算して教えるのが私、SLOPE関数で

b(切片)を計算して伝えるのが私、INTERCEPT関数です・・・。

SLOPEっていう単語は傾きとか勾配っていう意味があって、ほら回帰直線も傾いてるでしょ?これを計算するよ!

INTERCEPTはそのまま切片という意味の他に遮断する、遮るという意味があります。
1次方程式のxが0の時のy軸との交点を切片と言うので、回帰直線がy軸を遮断する点というイメージです。

スロープは建物の傾斜のついた通路、インターセプトはバスケットでパスを遮るプレイで聞きますね。

私達は第1引数として1次方程式のyの数値が入っているセル範囲、第2引数としてxの数値が入っているセル範囲を指定して貰えば、それぞれ傾きと切片を返すよ!

図の例の場合、計算したいのは人員数だから人員数がyになります。
計算したいものから先に教えて下さいね。

引数はかなりシンプルですね。
順番には気をつけます!

回帰直線は散布図の点と線の距離が最小になるように、最小二乗法という計算方法で計算されています。
これをSLOPEさんとINTERCEPTさんに頼らずに計算しようとするとなかなか大変です。

図の例では私が傾き0.1519、INTERCEPTが切片4.3696を答えとして返すから、引数として与えられた生産数と人員の回帰直線はy=0.1519x+4.3696になるよ。

求めたい生産数150個の時の人員数予測はxに150を入れて算出したyの値27.1546人・・・です。

実際には小数点以下の人員は配置できないので十分な人員の数は28人になりますね。

どう?私達のお仕事の凄さ、分かってもらえた?

なんとなく・・・難しいことが引数を指定して簡単にできることくらいは。

今の説明だけで理解するのは難しいと思うので、「SLOPE関数」「INTERCEPT関数」「回帰分析」などのワードで検索して理解を深めて下さい。

はい!

今回用いた図のように、散布図と回帰直線のグラフをエクセル上に作成する方法については下記リンクを参考にしてみて下さい。
【外部リンク】健康統計の基礎・健康統計学 – Excelで散布図と回帰直線を作成

私は回帰直線による予測はあくまで目安として考えています。
例えば今回の例で言うと、150個生産するには新たに別の生産場所が必要でその分人員も必要になるといった場合には、実際に必要な人員の数は予想よりも多くなることが想定されます。
予測に従うのではなく、予測値から外れた原因を考えることが大切です。

使えるようになる日は来るんでしょうか・・・

学習日数と習得具合を数値化したデータがあれば傾きと切片を求めて計算できるかも・・・です。

ベネ!
さっすがINTERCEPT!
まとめ
今回は使用する場面が限定的な2つのエクセル関数を紹介しました。
すぐに必要ではないかもしれませんが、頭の片隅に記憶して頂けるとふとした時に役立つかもしれません。
筆者の使用例ですが、今回の記事で挙げた例のように生産数150個の時に過去の実績を用いた回帰分析をして目安としての人数を算出しておき、配置人員計画や予算が適切なのかどうかを検討するのに使用しています。
もちろん、数字の上で計算された目安人数なので正しいとは言えません。大事なのは乖離についての理由を議論し把握しておくことだと考えています。
議論のたたき台としての目安を用意するのにSLOPE関数とINTERCEPT関数は大いに役立ってくれています。
記事の中では求めた傾きと切片を使って予測値を求めましたが、回帰直線を使った予測値を一気に求めて返すエクセル関数FORECAST関数が存在します。
傾きと切片を求める必要がなく、予測に使用するxと既知のx、既知のyが揃っている場合にはとても便利なので、存在だけでも知っておくと役に立つ時がくるかもしれません。
最小二乗法、回帰分析、単回帰分析、固変分解などの言葉が出てきた時に、もしこの記事で扱ったエクセル関数の存在を思い出してもらえたら幸いです!
最後まで読んで頂き、ありがとうございました!




コメント